벡터의 내적

벡터의 내적

제 1, 2 코사인 법칙

\(a = c \cdot \cos{B} + b \cdot \cos{C} \\ a^2 = b^2 + c^2 - 2bc \cdot \cos{A}\)

벡터의 내적 (제 2 코사인 법칙을 이용하여)

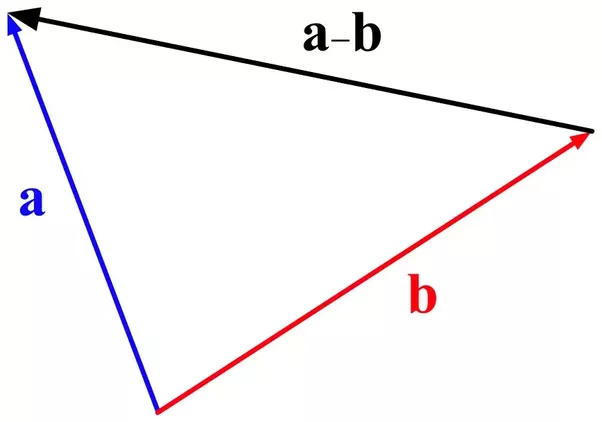\(\| \vec{a} - \vec{b} \|^2 = \| \vec{a} \|^2 + \| \vec{b} \|^2 - 2 \| \vec{a} \| \| \vec{b} \| \cos{\theta} \\ ( \vec{a} \ - \vec{b} ) \cdot ( \vec{a} - \vec{b} ) = \| \vec{a} \|^2 + \| \vec{b} \|^2 - 2 \| \vec{a} \| \| \vec{b} \| \cos{\theta} \\ \vec{a} \cdot \vec{a} - \vec{a} \cdot \vec{b} - \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b} = \| \vec{a} \|^2 + \| \vec{b} \|^2 - 2 \| \vec{a} \| \| \vec{b} \| \cos{\theta} \\ \| \vec{a} \|^2 - 2( \vec{a} \cdot \vec{b}) + \|b\|^2 = \| \vec{a} \|^2 + \| \vec{b} \|^2 - 2 \| \vec{a} \| \| \vec{b} \| \cos \theta \\ \vec{a} \cdot \vec{b} = \| \vec{a} \| \| \vec{b} \| \cos{\theta} \\ \cos{\theta} = \frac{ \vec{a} \cdot \vec{b}}{ \| \vec{a} \| \| \vec{b}\| } \\\)

Matrix notation

\(\vec{a} \cdot \vec{b} = \sqrt{\displaystyle\sum_{i=1}^{D} a_i^2} \times \sqrt{\displaystyle\sum_{i=1}^{D} b_i^2} \times \cos\theta = \sqrt{a^T a} \times \sqrt{b^T b} \times \cos{\theta} \\\) \(\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + \ldots + a_D b_D = \displaystyle\sum_{i=1}^{D} a_i b_i = \left(\begin{array}{cccc} a_1 & a_2 & \ldots & a_D \end{array}\right) \left(\begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_D \end{array}\right) = a^T b \\\) \(\cos{\theta} = \frac{a^T b}{\sqrt{a^T a} \times \sqrt{b^T b}} \approx \rho (correlation)\)